-Rプログラミング-【Statistics with “R”】How to use average in statistical computing?
いろいろな平均
-Rプログラミング-【Statistics with “R”】How to use average in statistical computing?
| コード | 意味 |
| mean(x) | xの平均を求める。 |
標本平均
データの位置を表す代表値のなかで最もポピュラーなのが標本平均だろう。
定義(標本平均)
大きさ\(n\)の標本\(x_1,…,x_n\)に対し、標本平均は
\[\bar{x}=\frac{1}{n}\left(x_1+…+x_n\right)=\frac{1}{n}\sum_{i=1}^n x_i\] で与えられる。
\[\bar{x}=\frac{1}{n}\left(x_1+…+x_n\right)=\frac{1}{n}\sum_{i=1}^n x_i\] で与えられる。
Rでは標本平均はmean( )を用いて計算できる。
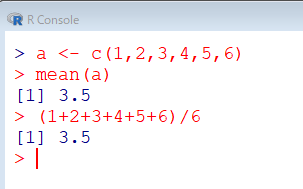
a <- c(1,2,3,4,5,6) mean(a) (1+2+3+4+5+6)/6
実行結果はこちら。
調和平均
定義(調和平均)
大きさ\(n\)の標本\(x_1,…,x_n\)に対し、調和平均は
\[H=\frac{n}{\frac{1}{x_1}+…+\frac{1}{x_n}}=\frac{n}{\sum_{i=1}^n \frac{1}{x_i}}\] で与えられる。
\[H=\frac{n}{\frac{1}{x_1}+…+\frac{1}{x_n}}=\frac{n}{\sum_{i=1}^n \frac{1}{x_i}}\] で与えられる。
調和平均は、一定距離を移動するときの速度の平均のように、逆数を足し合わせて基準となる値が定まる場合に用いられる。
Hsum <- function(x){ #x=(x_1,...,x_n)を代入すると調和平均を出力
n <- length(x)
n/sum(1/x)
}
a <- c(1,2,3,4,5,6,7,8,9,10)
Hsum(a) #aの調和平均
10/(1/1+1/2+1/3+1/4+1/5+1/6+1/7+1/8+1/9+1/10)
実行結果はこちら。

幾何平均
定義(幾何平均)
大きさ\(n\)の標本\(x_1,…,x_n\)に対し、幾何平均は
\[G=\sqrt[n]{x_1\cdot…\cdot x_n}=\left(\prod_{i=1}^n x_i \right)^{1/n}\] で与えられる。
\[G=\sqrt[n]{x_1\cdot…\cdot x_n}=\left(\prod_{i=1}^n x_i \right)^{1/n}\] で与えられる。
幾何平均は、GDPの平均増加率のように、データの相互の積を取って基準となる値が定まるときに用いられる。
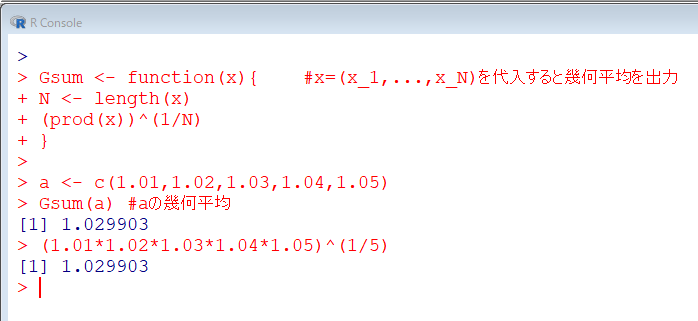
Gsum <- function(x){ #x=(x_1,...,x_n)を代入すると幾何平均を出力
n <- length(x)
(prod(x))^(1/n)
}
a <- c(1.01,1.02,1.03,1.04,1.05)
Gsum(a) #aの調和平均
(1.01*1.02*1.03*1.04*1.05)^(1/5)
実行結果はこちら。