共分散と相関係数 ~Rプログラミング~【Statistics with “R”】
データを分析では,同一の個体について複数の属性の情報を持った標本を扱うことが多い。このようなデータは以下のようにあらわせる。
k次元データ
定義(k次元データ)
同一の\(n\)個の個体に対して\(k\)個の変数について観測した結果
\[(x_{11},…,x_{1k}),…,(x_{n1},…,x_{nk})\]
を\(k\)次元データとよぶ。
k次元データをそのまま分析する前に,各変数間の関係に着目することが多い。この時に考えるのが2次元データとしての表現である。
2次元データ
定義(2次元データ)
同一の\(n\)個の個体に対して2つの変数について観測した結果
\[(x_1,y_1),…,(x_n,y_n)\]
を2次元データとよぶ。
共分散
2次元データの変数間の関係を把握するために,散布図を使って視覚的にアプローチする場合のほか,相関係数を使って,数として把握する方法がある。相関係数は,以下の共分散のアイディアを用いて表現される。
定義(標本共分散)
大きさ\(n\)の標本\((x_1,y_1,)…,(x_n,y_n)\)に対し,
\[\frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})\] を不偏標本共分散という。また,
\[\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})\] ただし\(\bar{x}=\frac{1}{n}\sum_{i=1}^n x_i,~\bar{y}=\frac{1}{n}\sum_{i=1}^n y_i\)である。
\[\frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})\] を不偏標本共分散という。また,
\[\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})\] ただし\(\bar{x}=\frac{1}{n}\sum_{i=1}^n x_i,~\bar{y}=\frac{1}{n}\sum_{i=1}^n y_i\)である。
共分散は
- 散布図でデータが右上がりに分布しているとき共分散は正の値になる。
- 散布図でデータが右下がりに分布しているとき共分散は負の値になる。
不偏標本共分散はRではcov( )関数で計算できる。
相関係数
定義(標本相関係数)
大きさ\(n\)の標本\((x_1,y_1,)…,(x_n,y_n)\)に対し,
\[r_{xy}=\frac{xとyの共分散}{xの標準偏差\times yの標準偏差}=\frac{\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum_{i=1}^n (x_i-\bar{x})^2 \sum_{i=1}^n (y_i-\bar{y})^2}}\] を標本相関係数という。 ただし\(\bar{x}=\frac{1}{n}\sum_{i=1}^n x_i,~\bar{y}=\frac{1}{n}\sum_{i=1}^n y_i\)である。
\[r_{xy}=\frac{xとyの共分散}{xの標準偏差\times yの標準偏差}=\frac{\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum_{i=1}^n (x_i-\bar{x})^2 \sum_{i=1}^n (y_i-\bar{y})^2}}\] を標本相関係数という。 ただし\(\bar{x}=\frac{1}{n}\sum_{i=1}^n x_i,~\bar{y}=\frac{1}{n}\sum_{i=1}^n y_i\)である。
- 散布図でデータが右上がりに分布しているとき相関係数は正の値になり、このとき正の相関があるという。
- 散布図でデータが右下がりに分布しているとき相関係数は負の値になり、このとき負の相関があるという。
相関係数は以下の性質を持つ。
標本相関係数の性質
標本相関係数は以下の性質を持つ。
\(|r_{xy}|\leq 1\)
\(r_{xy}=r_{yx}\)
\(|r_{(ax+b)(cy+d)}|=|r_{xy}|\)
\(|r_{xy}|\leq 1\)
\(r_{xy}=r_{yx}\)
\(|r_{(ax+b)(cy+d)}|=|r_{xy}|\)
標本相関係数はRではcov( )関数で計算できる。
Rでの共分散と相関係数の表示
Rでは不偏共分散のためににcov( )関数、相関係数のためにcor( )関数が用意されているが、定義に従って計算しても同様の結果が得られる。以下サンプルコード
#####データの生成####### N <- 100 #サンプルサイズ X <- runif(N,min=-1,max=1) #Xを一様分布から発生 Y <- runif(N,min=-1,max=1) #YをXとは別に一様分布から発生 #####分析############ plot(X,Y) #散布図 cov(X,Y) #共分散はcov(1個目の変数,2個目の変数)で計算できる cor(X,Y) #相関係数はcor(1個目の変数,2個目の変数)で計算できる cov(X,Y)/sd(X)/sd(Y) #相関係数はxとyの共分散をxの標準偏差とyの標準偏差で割ったもの (sum((X-mean(X))*(Y-mean(Y)))/(N-1))/(sd(X)*sd(Y)) #数式で直接計算しても同様の結果が得られる

ここではXとYを独立に設定した。散布図を見るとXとYの間に関係はみられず、相関係数は0になる。
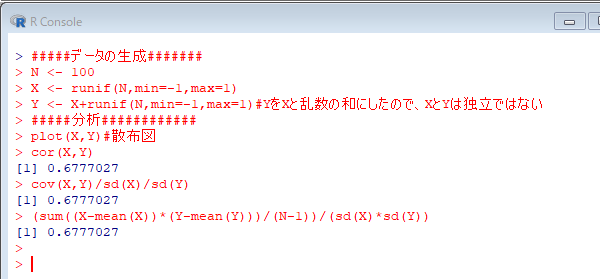
#####データの生成####### N <- 100 X <- runif(N,min=-1,max=1) Y <- X+runif(N,min=-1,max=1) #YをXと乱数の和にしたので、XとYは独立ではない #####分析############ plot(X,Y) #散布図 cor(X,Y) cov(X,Y)/sd(X)/sd(Y) (sum((X-mean(X))*(Y-mean(Y)))/(N-1))/(sd(X)*sd(Y))
ここではYをXと乱数の和として設定した。散布図を見るとXとYの間に右上がりの関係が見られ、相関係数は正になる。
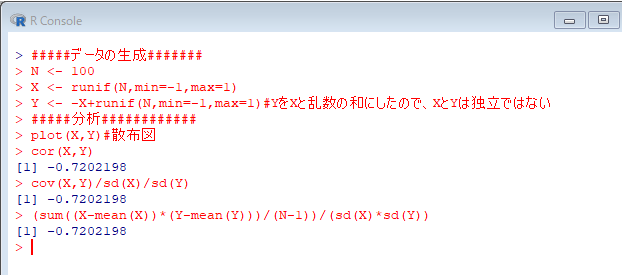
#####データの生成####### N <- 100 X <- runif(N,min=-1,max=1) Y <- -X+runif(N,min=-1,max=1) #YをXと乱数の和にしたので、XとYは独立ではない #####分析############ plot(X,Y) #散布図 cor(X,Y) cov(X,Y)/sd(X)/sd(Y) (sum((X-mean(X))*(Y-mean(Y)))/(N-1))/(sd(X)*sd(Y))
ここではYを-Xと乱数の和として設定した。散布図を見るとXとYの間に右下がりの関係が見られ、相関係数は負になる。