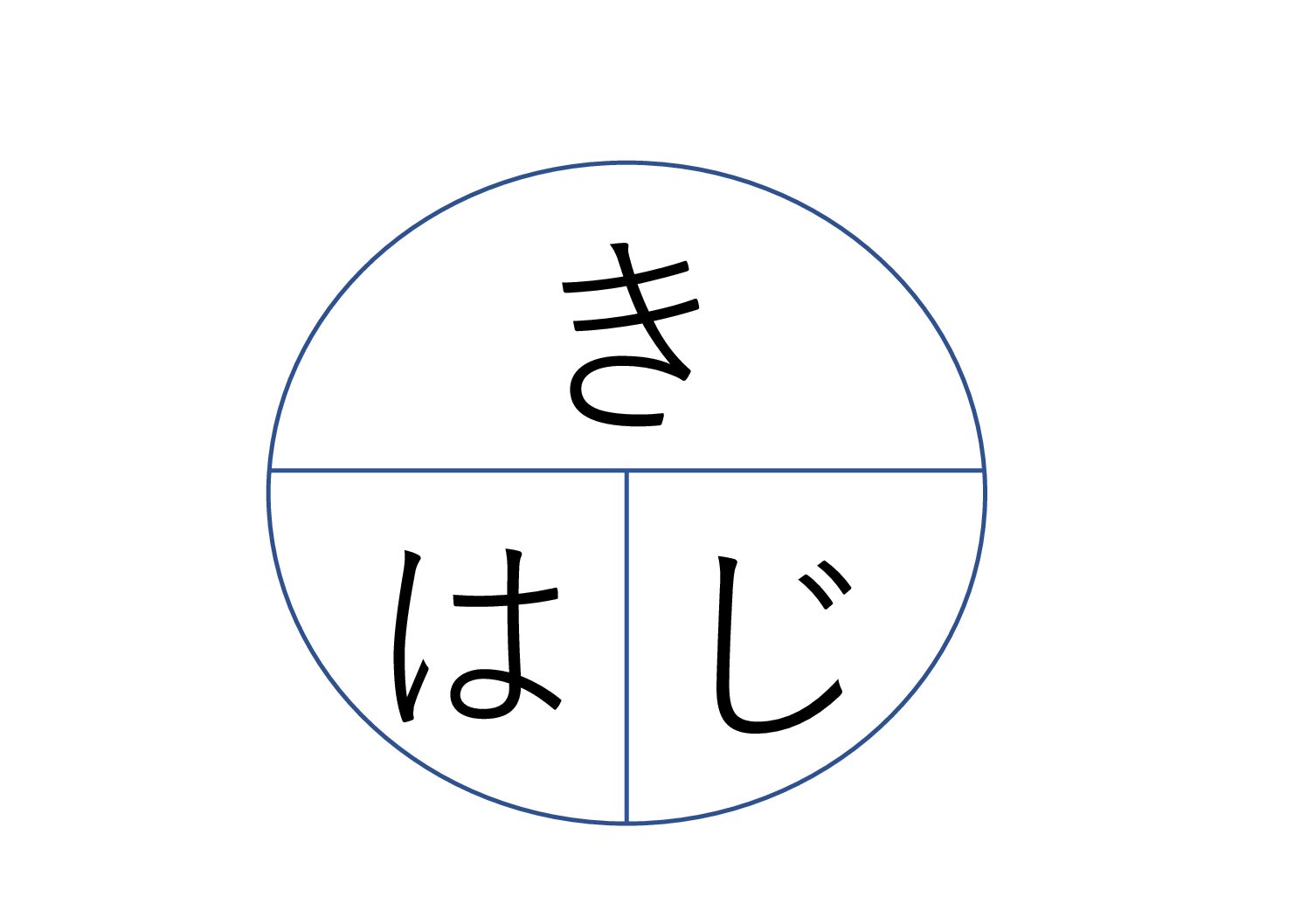
はじき(みはじ)問題
読者のみなさんは「はじき」や「みはじ」という言葉を聞いたことがあるでしょうか。「ドラえもんの鈴」と呼ぶ方もいらっしゃるようですが、この指導法には賛否両論あります。
小学校で速さなどの割合概念を教えるときに使用される道具で、「はやさ」「じかん」「きょり」のうち未知のものを隠し、既知のものに数字を書き入れることで、未知のものを計算できるようになっています。小学校においては割合でつまずく生徒が多く、問題を解けるようにしてあげるために効果的なことが分かっているので、「はじき/みはじ」による説明は、たくさんの先生が採用している指導法です。
実際、割合概念は小学生にとっては理解が難しいようです。とくに、小学校では方程式を十分に勉強せずに割合を勉強させますので、割合を理解するために必要なものを用意せずに割合を計算することが求められています。小学生が割合でつまずくことは、ある意味当然と言えるかもしれません。
割合の計算が出来るようになるので特に問題がないように思えるのですが、「みはじ/はじき」使用が中学校や高校の学習で問題を発生させるとも指摘されています。
彼らの懸念の1つは、「はじき/みはじ」の利用で、生徒が割合概念の理解と全く関係なく計算だけできるようになり、利用を継続しても、生徒の割合概念の理解を全く促されないという点にあるようです。中学校以降で出現する割合を用いた概念の習得を著しく妨げ、生徒の成績向上などの足を引っ張っていると主張しています。例えば理科で学習する「オームの法則」はその一つで、電圧と、電流と抵抗の積との等式です。等式によって記述される法則ですので、方程式の計算規則に従うわけで、その計算は簡単なはずなのですが、「はじき/みはじ」のような道具がないと計算できないという生徒が大量に発生しており、指導が困難になっていると言われています。
2つ目に懸念されることは、「みはじ/はじき」のような道具は概念の拡張に弱いことです。道のりが速さと時間の積になるという関係は、比例関係であり、比例関係は一次関数の特殊ケースです。実際、中学校に進むと、道のりが速さと時間の積になるという関係は、あらたに「位置」という概念をくわえて1次関数の文脈で用いられるようになり、中学校の理科では、さらに「加速度」という概念をくわえて2次関数の文脈で用いられるようになります。概念自体を理解してしまえば計算は難しくないのですが、「みはじ/はじき」ユーザーにとっては、同時に扱わなくてはならない概念が増えていくと、「みはじ/はじき」のような図は大量にに必要になります。その結果、どこかで完全に歯が立たなくなってしまい、ドロップアウトしてしまうようです。実際に使ってみると歯が立たなくなる理由もわかるでしょう。
このように、悪名高い「みはじ/はじき」なのですが、小学校の現場では、やむを得ず使用されているという側面もあるようです。すでに言及したように、小学校では方程式の学習を十分に行わずに、割合の計算ができるようになることが目指されています。しかし、割合概念自体が等式の使用に依存しているので、生徒たちが自信をもって「分かる」ためには、方程式の操作か、それに準じる具体的なイメージの形成が不可欠です。これは小学生にとっては大変なことです。先生が生徒一人ずつと対話して、理解に誤解がないかを点検し、誤解があればどこに誤解があるのかを説明し、納得させ、反復練習しなければいけません。割合概念を小学生に理解させるためには、かなりの時間と労力が必要になります。
一方で、社会でも広く認知されているように、小学校の先生の負担は相当のものです。生徒のレベルは様々ですし、一人でほとんどすべての教科を教えなくてはいけないうえ、英語やプログラミングなど教科数も増えています。さらに授業以外の負担も相当あると指摘されています。また、小学生は大人ほど論理的に考える訓練を受けていませんので、発達段階に配慮しながらも正しい理解に導くよう、細心の注意を払わなくてはなりません。
この状況で、割合の理解のために十分な時間を用意してほしいというのは、現実的ではないでしょう。もちろん先生方の数学の理解のレベルが上がれば、教育の質は上がるかもしれませんが、日本全体でこのような問題が緩和されていくためには、小学校の先生方の負担を相当量削減するしかないのではないかな、と思います。


「はじき(みはじ)問題」への2件のフィードバック
コメントは受け付けていません。