
~数学で用いられる関数~
Rプログラミング
~数学で用いられる関数~
三角関数
R言語で三角関数をあらわすにはこれらの関数が使えます。三角関数にはsinやcosやtanなどがありますが、いずれもRで計算可能です。たとえばRでsin(pi/2)と入力すると1という値を返してくれます。三角関数のグラフを書きたい場合にはcurve関数と組み合わせることで関数のグラフを確認することができてとても便利です。
| 関数 | 数学での意味 | グラフを書くコードの例 |
| sin(x) | sin x | curve(sin,-2*pi,2*pi) |
| cos(x) | cos x | curve(cos,-2*pi,2*pi) |
| tan(x) | tan x | curve(tan,-2*pi,2*pi) |
| asin(x) | arcsin x | curve(asin,-1,1) |
| acos(x) | arccos x | curve(acos,-1,1) |
| atan(x) | arctan x | curve(atan) |
asinやacosなどはsinやcosの逆関数です。但し、逆関数が存在するためには単調増加や単調現象の条件が必要なので、これらの三角関数の逆関数の定義には注意が必要です。
定義(逆三角関数)
\(\sin{x}\hspace{3mm}(-\pi/2 \leq x \leq \pi/2)\)の逆関数を \( \sin^{-1}{x}\hspace{3mm}(-1\leq x \leq 1)\)や\(\arcsin{x}\) と書く。
\(\sin{x}\hspace{3mm}(0 \leq x \leq \pi)\)の逆関数を \( \sin^{-1}{x}\hspace{3mm}(-1\leq x \leq 1)\)や\(\arccos{x}\) と書く。
\(\tan{x}\hspace{3mm}(-\pi/2 \leq x \leq \pi/2)\)の逆関数を \( \tan^{-1}{x}\hspace{3mm}(-\infty< x < \infty)\)や\(\arctan{x}\) と書く。
\(\sin{x}\hspace{3mm}(0 \leq x \leq \pi)\)の逆関数を \( \sin^{-1}{x}\hspace{3mm}(-1\leq x \leq 1)\)や\(\arccos{x}\) と書く。
\(\tan{x}\hspace{3mm}(-\pi/2 \leq x \leq \pi/2)\)の逆関数を \( \tan^{-1}{x}\hspace{3mm}(-\infty< x < \infty)\)や\(\arctan{x}\) と書く。
双曲線関数
R言語で双曲線関数をあらわすにはこれらの関数が使えます。双曲線関数にはsinhやcoshやtanhなどがありますが、いずれもRで計算可能です。双曲線関数のグラフを書きたい場合にはcurve関数と組み合わせることで関数のグラフを確認することができてとても便利です。
| 関数 | 数学での意味 | グラフを書くコードの例 |
| sinh(x) | sinh x | curve(sinh,-3,3) |
| cosh(x) | cosh x | curve(cosh,-3,3) |
| tanh(x) | tanh x | curve(tanh,-3,3) |
| asinh(x) | arcsinh x (sinh xの逆関数) | curve(asinh,5,5) |
| acosh(x) | arccosh x(cosh xの逆関数) | curve(acosh,1,5) |
| atanh(x) | arctanh x(tanh xの逆関数) | curve(atanh,-1,1) |
定義(双曲線関数)
\(x\in \mathbb{R}\) に対し,
\[\sinh{x}=\frac{e^x-e^{-x}}{2}\]
\[\cosh{x}=\frac{e^x+e^{-x}}{2}\]
\[\tanh{x}=\frac{\sinh{x}}{\cosh{x}}=\frac{e^x-e^{-x}}{e^x+e^{-x}}\]
を双曲線関数 (hyperbolic function)という。
平方根・対数関数
Rで平方根や対数関数をあらわすにはこれらの関数が使えます。例えば平方根はsquare rootといい、その略でRでは平方根をsqrtと書きます。底を書かないlogはRでは自然対数を表します。底が2や10のようなときの対数をRではlog2やlog10で表現します。
| 関数 | 数学での意味 | グラフを書くコードの例 |
| sqrt(x) | xの平方根 | curve(sqrt,0,5) |
| log(x) | 対数(底:e) | curve(logx,0,5) |
| log2(x) | 対数(底:2) | curve(log2,0,5) |
| log10(x) | 対数(底:10) | curve(log10,0,5) |
指数関数
Rで指数関数を表すには以下のコードが使えます。
対数関数ではなく指数関数を使いたい場合はどうしたらよいでしょうか。
指数関数の定義に従って、自分でaのx乗の関数
を作ってみましょう。
expax <- function(a,x) a^x
expax(2,1)
expax(2,2)
expax(2,3)
expax(3,1)
expax(3,2)
expax(3,3)
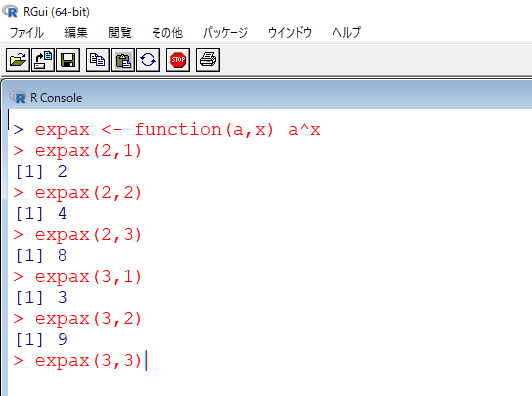
このように、「function」を使用することで、あらかじめ定義されていない関数も自作することが出来ます。

