Rの基本 分散と標準偏差
データの散らばりを表す代表値に,分散と標準偏差があります。
分散
分散とは,データの「バラつきの大きさ」「散らばりの大きさ」を表す指標。
- 分散が大きい → バラつきが大きい,平均から遠いものが多い
- 分散が小さい → バラつきが小さい,全部が平均に近い,まとまっている
定義(標本分散)
大きさ\(N\)のデータ\(x_1,…,x_N\)が与えられたとする。このとき,標本分散は\[\frac{1}{N}\sum_{i=1}^N \left(x_i-\bar{x}\right)^2\]
で与えられる。ただし\(\bar{x}\)は\(x_1,…,x_N\)の標本平均である。
サンプルサイズが大きいときは標本分散で十分だが,サンプルサイズが小さいときには標本分散では正確にデータの「バラつきの大きさ」「散らばりの大きさ」を表せない場合がある。
そのため,標本不偏分散が用いられる場合がある。
定義(標本不偏分散)
大きさ\(N\)のデータ\(x_1,…,x_N\)が与えられたとする。このとき,標本分散は\[\frac{1}{N-1}\sum_{i=1}^N \left(x_i-\bar{x}\right)^2\]
で与えられる。ただし\(\bar{x}\)は\(x_1,…,x_N\)の標本平均である。
Rには標本不偏分散を計算するためにvar( )関数が用意されている。
もちろん定義に従って計算しても,同じ結果が得られる。
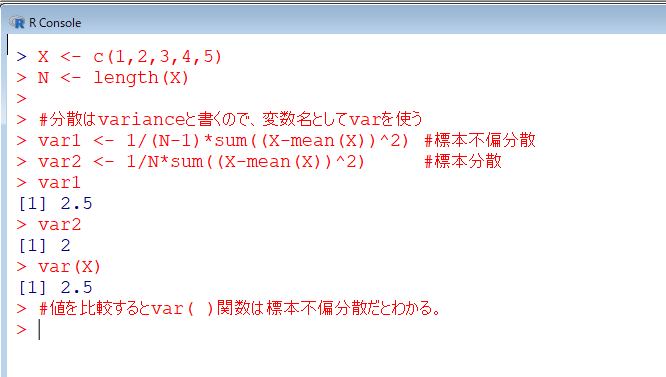
X <- c(1,2,3,4,5) N <- length(X) #分散はvarianceと書くので、変数名としてvarを使う var1 <- 1/(N-1)*sum((X-mean(X))^2) #標本不偏分散 var2 <- 1/N*sum((X-mean(X))^2) #標本分散 var1 var2 var(X) #値を比較するとvar( )関数は標本不偏分散だとわかる。
計算結果はこちら
標準偏差
分散とは,データの「バラつきの大きさ」「散らばりの大きさ」を表す指標で、分散の平方根を取った値。そのため,
- 標準偏差が大きい → バラつきが大きい,平均から遠いものが多い
- 標準偏差が小さい → バラつきが小さい,全部が平均に近い,まとまっている
定義(標本標準偏差)
大きさ\(N\)のデータ\(x_1,…,x_N\)が与えられたとする。このとき,標本標準偏差は\[\sqrt{\frac{1}{N}\sum_{i=1}^N \left(x_i-\bar{x}\right)^2}\]
で与えられる。ただし\(\bar{x}\)は\(x_1,…,x_N\)の標本平均である。
分散の場合と同様に,サンプルサイズが小さいときには標本標準偏差では正確にデータの散らばりを表せない場合がある。
そのため,標本不偏標準偏差が用いられる場合がある。
定義(標本不偏標準偏差)
大きさ\(N\)のデータ\(x_1,…,x_N\)が与えられたとする。このとき,標本標準偏差は\[\sqrt{\frac{1}{N-1}\sum_{i=1}^N \left(x_i-\bar{x}\right)^2}\]
で与えられる。ただし\(\bar{x}\)は\(x_1,…,x_N\)の標本平均である。
Rには標本不偏標準偏差を計算するためにsd( )関数が用意されている。
定義に従って計算しても,同じ結果が得られる。
#標準偏差はstandard deviationと書くので、変数名としてsdを使う sd1 <- sqrt(var1) #標本不偏標準偏差(分散の平方根square root) sd2 <- sqrt(var2) #標本標準偏差 sd1 sd2 sd(X) #値を比較するとsd( )関数は標本不偏分散だとわかる。
