
~Rプログラミング~【Statistics with “R”】
四分位数
~Rプログラミング~【Statistics with “R”】
定義(四分位数)
大きさ\(n\)の標本\(x_1,…,x_n\)に対し,これらを小さい順に並べたものを,\(x_\left(1\right),…,x_\left(n\right)\)と表す。さらに
\[q(r)=\left\{ \begin{array}{l} x_{(r)} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~rが自然数のとき\\ (\lceil r \rceil-r )x_{(\lfloor r \rfloor )}+(r-\lfloor r \rfloor )x_{(\lceil r \rceil )}~~~rが自然数でないとき \end{array} \right. \] このとき
\[q((n+3)/4)\] を第一四分位数, \[q((3n+1)/4)\] を第三四分位数という。
\[q(r)=\left\{ \begin{array}{l} x_{(r)} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~rが自然数のとき\\ (\lceil r \rceil-r )x_{(\lfloor r \rfloor )}+(r-\lfloor r \rfloor )x_{(\lceil r \rceil )}~~~rが自然数でないとき \end{array} \right. \] このとき
\[q((n+3)/4)\] を第一四分位数, \[q((3n+1)/4)\] を第三四分位数という。
Rでは、summary関数を実行することで、これらの四分位数を計算することが出来る。いっぽうで、定義に従って計算しても同様の計算結果を得ることが出来る。
q <- function(x,r){
order_stat <- sort(x) #xを小さい順に並べる
if(r%%1==0){ #1で割った余りが0か否かで自然数か否かを判別
qr <- order_stat[r] #rが自然数の場合
}else{
ceil_r <- ceiling(r) #rが自然数でない場合
floor_r <- floor(r)
qr <- (ceil_r-r)*order_stat[floor_r]+(r-floor_r)*order_stat[ceil_r]
}
qr
}
Q3 <- function(x){
n <- length(x)
q(x,(3*n+1)/4)
}
Q1 <- function(x){
n <- length(x)
q(x,(n+3)/4)
}
X <- rnorm(100) #検証用データ
Q3(X) #第三四分位数
Q1(X) #第一四分位数
summary(X) #Rの組み込みsummary関数との比較
計算結果はこちら。
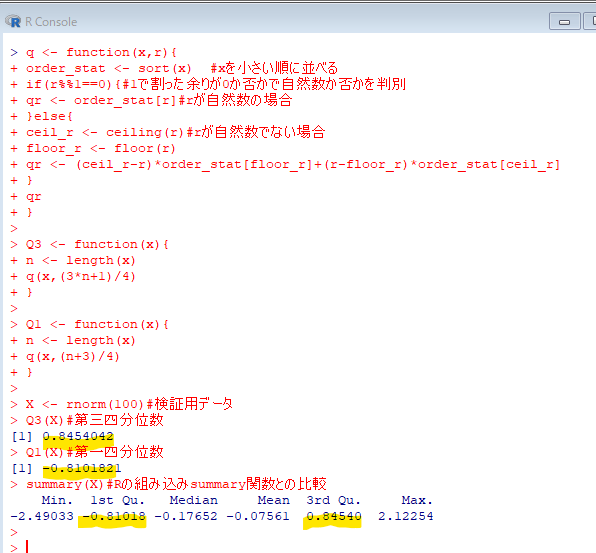
計算結果が一致している。